테브난 등가 회로는 복잡한 회로를 훨씬 더 간단하게 해석하는 데 사용되는 유용한 이론입니다.
노턴 등가 회로는 같은 이론의 다른 표현이라고 생각하셔도 문제없습니다.
택배를 보내려면 받는 사람이 어떤 사람이냐 보다는 실제 주소, 전화번호, 이름이 가장 중요하겠죠!
회로에서도 마찬가지로 역할이 다른 파트들을 합칠 때 가장 중요한 정보인
입출력 저항(Rt), 오픈 전압(Voc), 쇼트 전류(Isc)를 테브난 등가 회로를 통해 알아낼 수 있습니다!

왜 저 세 가지 정보가 중요한지 알아보기 위해 쉬운 예를 보겠습니다!
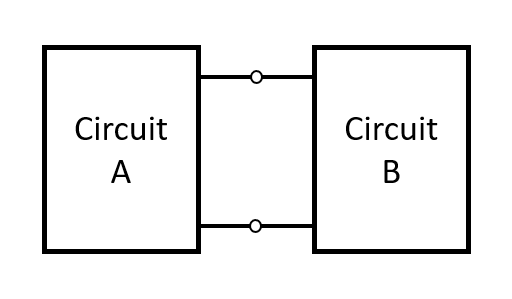


모든 회로는 위처럼 회로 A와 회로 B의 연결로 볼 수 있습니다.
회로 B를 RL(3kΩ)에 3V 이상의 전압이 걸리 때 불이 들어오는 LED라고 생각해보겠습니다.

Vs를 3V의 전압원을 주면 RL에는 3k/(Rs+3k) * 3V 만큼의 전압이 걸려 Rs>0 이면 LED에 불이 들어올 수 없습니다.
이 때문에 항상 소스의 출력 전압인 Rs는 작게 로드의 저항 RL은 크게 만드는 게 중요합니다!
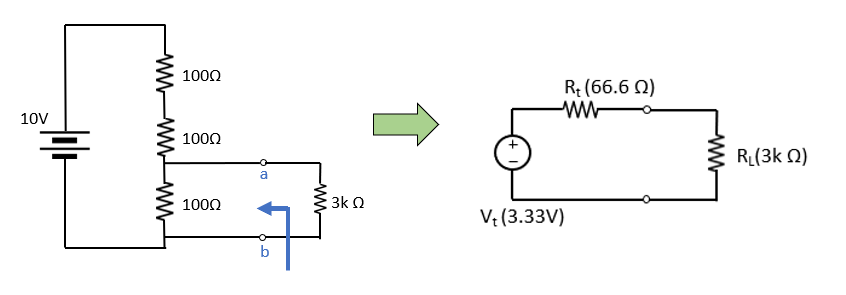
실제 회로에서는 입력과 출력 모두 복잡하기 때문에 테브난 등가 이론을 이용해 위 마지막 그림처럼 만들어주는 게 중요한 거죠!
지금까지 테브난 이론이 무엇인지, 왜 필요한지에 대해 알아보았으니 실제 변환 방법과 예제를 풀어보도록 하겠습니다!

테브난 등가 회로로의 변환은 다음과 같이 세 단계로 쉽게 구할 수 있습니다.
1. 독립전원(indipendent source) 분리
2. 테브난 전압 구하기
3. 테브난 등가 저항 구하기

첫 번째,
각각의 독립전원들은 중첩의 원리(superposition principle)에 의해 각각 계산한 것의 합과 같습니다.
독립 전압 전원(Independant voltage source)은 단락(short)시키고
독립 전류 전원(Independant current source)는 개방(open)시키도록 합니다.
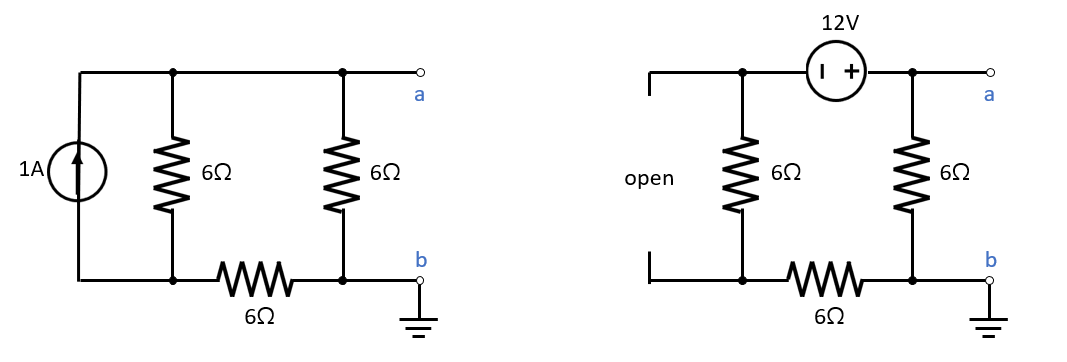
두 번째,
테브난 등가 회로의 포인트는 어디서 바라보는지입니다!
다른 부가적인 회로를 붙일 부분을 정하고 외부 회로 입장에서 회로 A부분의 세 가지 요소를 구하기 때문입니다.
따라서 노드 a, b사이의 전압 Vab를 구해주면 됩니다.
(1) 전류 소스 회로에 의한 Vab(1)

다음과 같이 전류 소스 회로를 재구성하면 쉽게 알아볼 수 있습니다.
노드 a, b사이 저항값과 흐르는 전류를 곱하면 전압 Vab를 구할 수 있는데
전류는 6Ω 의 저항이 있는 A와 12Ω저항이 있는 B에 분배되어
1A * 6Ω/(6Ω + 12Ω) = 1/3A의 전류가 b에서 a로 흐릅니다.
따라서 전압 Vab는 - 6Ω * 1/3A = -2V가 됨을 알 수 있습니다.
(2) 전압 소스에 의한 전압 Vab(2)
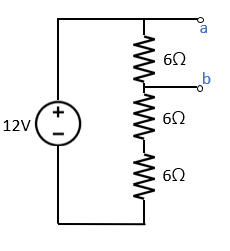
위와 같이 회로를 재구성하면 Vab는 12V * 6Ω/(6Ω + 6Ω + 6Ω) = 4V 임을 구할 수 있습니다.
따라서 테브난 전압 Vt = Vab(1) + Vab(2) = -2V + 4V = 2V입니다.
세 번째,
마지막으로 외부에서 바라본 저항을 구해주면 됩니다.
마찬가지로 모든 전원들을 없애주고,
노드 a,b를 기준으로 직렬, 병렬회로를 그려주시면 쉽게 구할 수 있습니다.
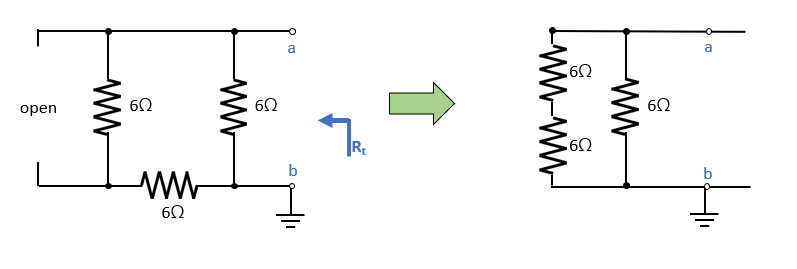
위와 같이 재구성 후 합성 저항을 구해주면 밖에서 바라본 테브난 저항은
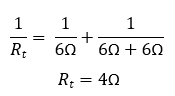
따라서 다음과 같이 테브난 저항 Rt는 4Ω, 테브난 전압 Vt는 4V인 등가 회로를 구성함을 알 수 있습니다.

노턴 등가 회로는 전류 소스와 등가 저항으로 이루어지는데,
노턴 전류 In = Vt / Rt로 구할 수 있습니다.

이를 통해 회로 외부에서 바라본 입출력 저항(Rt) = 4Ω, 오픈 전압(Vt) = 4V, 쇼트 전류(In) = 1A 임을 확인할 수 있습니다.
추가로 모르겠는 부분, 잘못된 점 언제든지 댓글로 남겨주세요!
피드백은 언제나 환영입니다~~ +_+
도움이 되셨다면 좋아요 부탁드립니다!